
Aero-Elastic Behavior of Aerial-Aquatic Robots
February 2024 - June 2024

I took part in a research project at EPFL whose aim was to model the mechanical behavior of a wing in oscillatory motion and to reconstruct the deformations with an experiment.
The ultimate goal is to add this mechanical coupling to the open-source Ptera Software solver, which can quickly calculate the aerodynamic forces acting on the wings of a biomimetic drone.
My project was supervised by Raphael Zufferey , now assistant professor at MIT, in the Laboratory of Intelligent Systems.
Modeling
Using my knowledge of continuum and rigid body mechanics, I managed to find the partial differential equation modeling the torsional deformation of the leading edge. I discovered an article in the literature that derived a similar equation. Let's start by introducing the variables:
- flapping angle
- torsion angle
- surface density of the membrane
- chord length
- half-span
- surface aerodynamic forces
The goal was to develop a simple deformation model. The wing is made of a carbon tube at the leading edge, and a membrane held by a light carbon frame. The stiffness of the wing comes from the carbon tube and the aerodynamic forces are generated by the membrane.
When the wing is flapping, it appears that it is twisted. It led me to think that the deformation could come from a torsion model. So, I focused on building one.
The rigid body laws cannot be applied to the carbon tube as it is twisting but they can be applied on infinitesimally small parts of the carbon tube and the membrane. It will lead to a PDE instead of an ODE.
The kinematic model of the isolated infinitesimally small length of the tube can be seen on the right schema.
My derivations gave the following partial differential equation modelling the torsion deformation of the wing :
Results
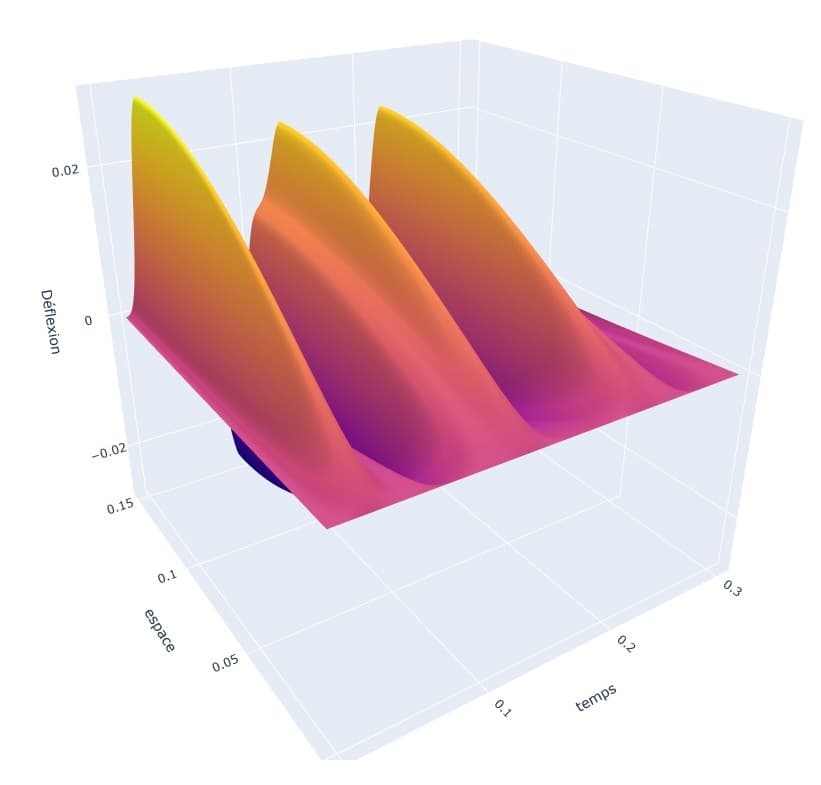
Using the finite difference method, I solved the PDE for the case of a wing in a vacuum. The graph represents the time evolution of the torsion angle at different points of the wing. The surface represents the deflection of the trailing edge for a wing flapping in a vacuum.
Numerical Reconstruction

Using a method called digital image correlation, I tried to reconstruct the deformation of the wings in motion on a computer. I found the software MultiDIC that has been developed for reconstructing 3D shapes with multiple cameras.
For my goal, I needed two cameras and a speckled pattern to paint on the membrane that serves as a wing.
As the preprocessing step was really long for MultiDIC, I created a software that speeds it up by automatically synchronizing the videos with a clap and generating the useful frames.
